Kaip rasti lygiakraščio trikampio plotą

Matematika ir ypač geometrija, pagalApklausa moksleiviams, vienas iš labiausiai nepatiko pamokų, ir visi, nes jie yra priversti išmokti didelį skaičių formules, kurios yra 90% šiandienos suaugusiems gyvenime neradau praktinį taikymą. Bet, už momentą, mes mokome formules, spręsti problemas, kad lygtis yra ne tam, kad jie gali praversti gyvenime, ir todėl, kad ji vystosi mąstymą ir logiką. Net senovės graikų išminčiai sakė, kad žmogaus intelektas gali būti matuojamas pagal matematikos žinias. Ir kai jūs nusprendėte susipažinti su į lygiašonio trikampio formulių taikymo - mes save į rankas ir skaityti visą straipsnį.
Prieš pradėdami atsakyti į klausimą, kaip rastivienodo laipsnio trikampio plotas ir eikite į praktinę straipsnio dalį, kur pateikiamos formulės ir skaičiavimai, leiskite mums pačiam apibūdinti pačią sampratą. Vientisas trikampis yra trikampis, kuriame dvi iš trijų pusių yra vienodi ilgio, vadinami šoninėmis pusėmis. Tais atvejais, kai yra įprastas trikampis, kuriame visos pusės yra lygios, jis taip pat laikomas lygiaverčiu, bet atvirkščiai, kai lygiagretus trikampis laikomas teisingu - tai klaidinga.
Turėtų būti pažymėtos trikampio pusės, mes tai padarysime taip, kaip parodyta paveikslėlyje žemiau, kur: a - pusės, b-bazė ir h aukštis.

Kaip apskaičiuoti lygiakraščio trikampio plotą, formules.
Įrašę aukštį, kampus ir kampą, galime pradėti spręsti problemą.
Pirmiausia mes nustatysime, ką mes žinome.
Jei aukštis ir apačia - tada klasikinė formulė (* - daugybos ženklas):
S = ½ * b * h
Pavyzdžiui, pakeiskime skaičius, kur: h = 16, b = 18, mes gauname tokį:
S = ½ * 18 * 16 = 9 * 16 = 144;
Vienalaikio trikampio plotas yra S = 144 cm2
Yra ir kitos formulės, kurios mums padėskaip sužinoti lygiagrečiojo trikampio plotą. Viena iš tokių formulių yra Herono metodas. Nereikime rašyti sudėtingos formulės, mes priimsime pagrindą, sutrumpintą:
S = ¼ b √4 * a2-b2
Akivaizdu, kad b yra pagrindas ir - lygios pusės. Formulė yra tinkama tais atvejais, kai h aukštis nežinoma.
Vertindami vertes, tegul a = 6, b = 3 gauname tokį:
S = ¼ * 3 √4 * 62-32 = ¾ √144-9 = ¾ * 9 = 8,7
Galite apskaičiuoti plotą, kuris yra lygus trikampio kraštams ir kampui tarp šonų:
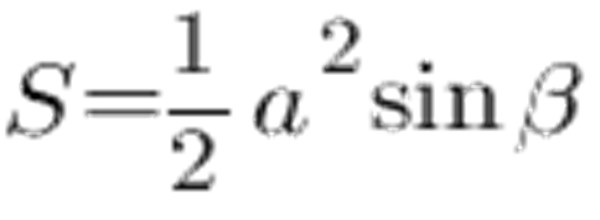
Pagal sinuso stalą 45 ° kampas lygus 0.7071, šoninis a ir tegul jis yra 6 cm, mes gauname:
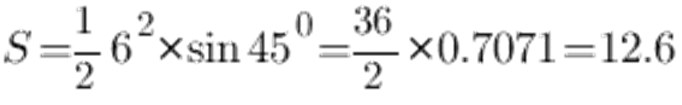
Dėl to vienodo laipsnio trikampio plotas yra 12,6 cm2.
Taip pat yra būdų apskaičiuoti plotą, įskaitantįskaitant lygiakraščio trikampio atveju, tačiau jie yra gana sudėtingi ir netaikomi "elementariems" skaičiavimams, pvz., pateiktiems aukščiau, sudėtingos matematikos sąvokoje. Ir nereikia kalbėti apie dalykus, kurių net mokytojai su patirtimi nesupras.
Taigi, jūs galite kvėpuoti atodūsio atleidimąmažas geometrijos kursas, skirtas rasti lygiagrečiojo trikampio plotą, bus laikomas užbaigtu, o žinių, gautų skaitant straipsnį, išmokta "penkiais".














